CNN Part - I
10 Nov 2017
Before we jump into the full convolutional neural network, lets first understand the basic underlying concept and then build up on that.
This post will take the following approach to explainations :
- Convolution Concept
- Convolutional Neural Network
- Strided Convolutions
Convolution Concept
For those of you who have taken a class/course on digital signal/image processing, would be comfortable with the concept of covolution. For the rest of us, let quickly run through the concept, so that we can dive into the actual cnn implementation.
If you have an image of a city with alot of buildings as below, and you would like to extract all the edges from the image, how would you do it?

Whenever one signal(S) needs to be modified to extract only a set of desired features from it, the process is known as filtering. Now to carry of filtering, another set of signals are required which we somehow imposed/applied over the original signal S,called filters (F).
These filters can also be called masks, as they help us “mask” all image features except the ones we want!
Now all the masks can show the required effect on the image if they are convolved with the images pixels in a manner demonstrated by the below animation.
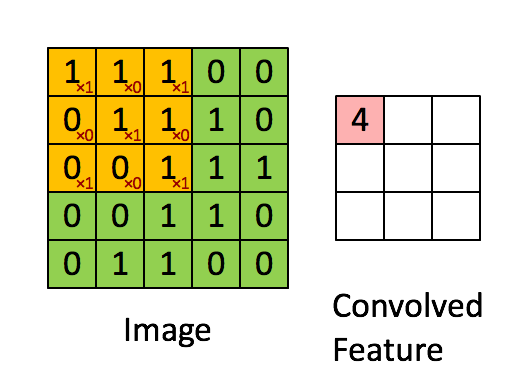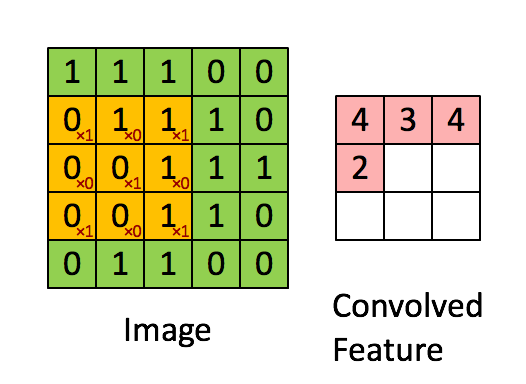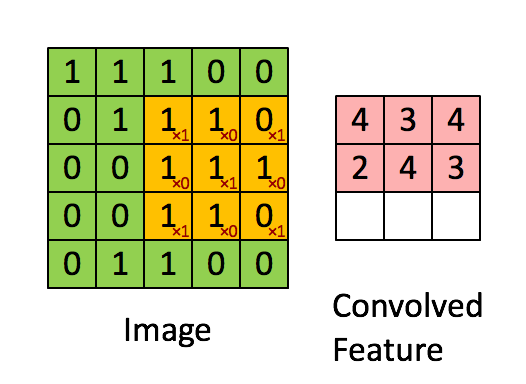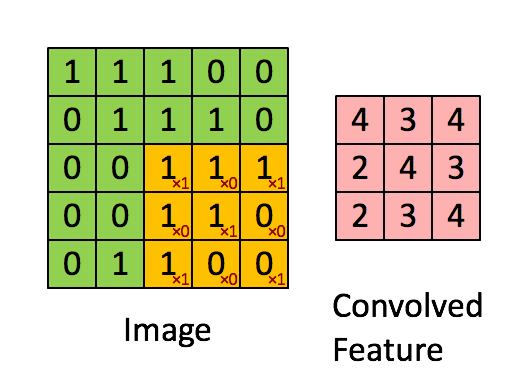
For better understanding of convolution please refer to this post.
Convolutional Neural Network
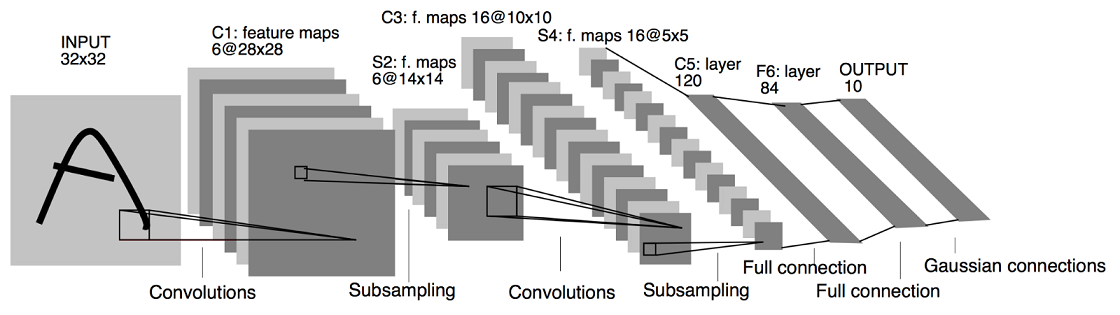
The above illustration from teh original paper by Prof Yann Lecun shows all the basic components and data flow in a convolutional network.
To put it in a quanitifiable form, every CNN has the following components/layers:
- Input image
- Convolution layer
- Pooling Layer (max pooling or avg pooling)
- Flattening
- Fully connected Layer (default neural network)
We will dive deeper into the details of each of the above layers in subsequent posts.
Strided Convolutions
When we are dealing with convolution on images of very large size, its not always required to convolve over each and every pixel of an image. So we can set the subsequent convolutions to be shifted by more than one pixel in either the vertical or horizontal axis.
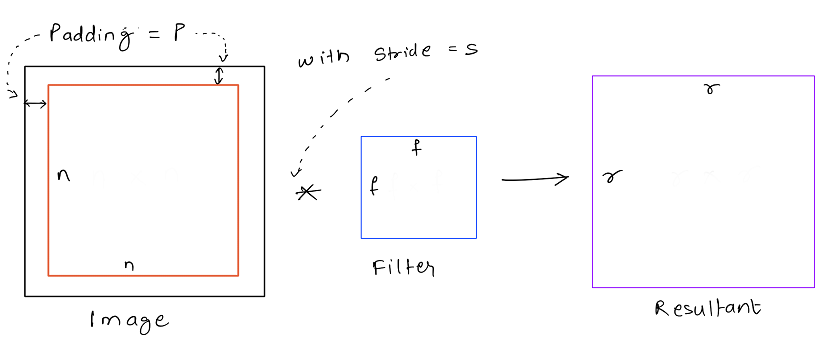
This shift in subsequent convolutions is called the stride, and hence the name strided convolutions.
If we have an image of dimension n x n with a padding p, which is convolved with filter of dimension f x f witha stride of s, then the output dimensions can be determined using the below general equation:
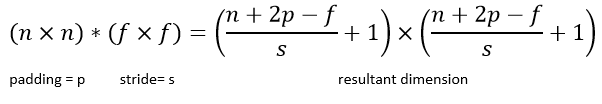
Link to part II
PS: In the mathematical covolution operation we flip one of the signals being convolved i.e. like viewed in a mirror. The operation we are using above is actually cross-correlation, but generally in deep learning convolution is the term used for it!